Տնային աշխատանք

Posted by jannanavoyan

Տնային աշխատանք

Posted by jannanavoyan

N217

ա) f(x) = x² (n g(x)=√x

_w) F=fog

F = (√x)² = x

D(F) = [0; +∞0)

բ) F=g of

F = √x² = |x|

D(F) == 00: + ∞0) => R

դ) F = fof

F = (x²)² = x²

D(F) = ER

N216

ա)F(x)=F(x-1)

x = 1

x in[0,1]

բ)F(x)=f(2x)

f(x) = 1/2

x in[-0,5,0]

գ) F(x) = f(- x ^ 2)

x in[-1;1]

N218

ա) x – 8x +21= x² = 8x + 16 + 5 = (x-4)² + 5 =>

x² – 8x + 21 = (x-4)² + 5

բ) 4x2x²-2=-2 (x² – 2x + 1) ==2(x – 1)² =

= (-1)²-(-2) =>

2x² -2=(x-1)²-(-2)

գ) 3x² – 6x – 10 = 3x² – 6x + 3 – 1 3 = 3(x² – 2x + 1) – 13 =

= 3(x – 1)² – 13 => 3x – 6x – 10 = 3(x-1) ² – 13

Կրկնակի անկյան սինուսն ու կոնսինուսն, տանգեսն ու կոտանգես

Posted by jannanavoyan

cos2a=cos²a-sin²a

cos2a=1-2sin²a

cos2a=2cos²a-1

sin²a=2sinacosa

tg2a=2tga/1-tg²a

ctg2a=ctg²a-1/2ctga

իջեցման բանձևեր

sin²a=1-cos2a/2

cos²a=1+cos2a/

Տնային աշխատանք

Posted by jannanavoyan

Վարժ. 126ա) cos(π/4-α)=cosπ/4 cosα + sinπ/4 sinα=√2/2 × cosα + √2/2 sinα=(cosα+sinα)√2/2

բ) cos(π/4+α)=cosπ/4 cosα – sinπ/4 sinα=√2/2 × cosα – √2/2 sinα=(cosα-sinα)√2/2

գ) sin(π/4-α)=sinπ/4 cosα – cosπ/4 sinα=√2/2 × cosα – √2/2 sinα=(cosα-sinα)√2/2

դ) sin(π/4+α)=sinπ/4 cosα + cosπ/4 sinα=√2/2 × cosα + √2/2 sinα=(cosα+sinα)√2/2

ե) tg(π/4+α)=tgπ/4+tgα / 1-tgπ/4tgα=1+tgα/1-tgαզ) tg(π/4-α)=tgπ/4-tgα / 1+tgπ/4tgα=1-tgα/1+tgα

Վարժ. 129ա) √2 sin(π/4+α)-sinα=√2(sinπ/4+cosα + cosπ/4 sinα)-sinα=2(cosα+sinα)/2 – sinα=cosα+sinα-sinα=cosα

բ) √2 cos(π/4-α)-cosα=√2(cosπ/4+cosα + sinπ/4 sinα)-cosα=2(cosα+sinα)/2 – cosα=cosα+sinα-cosα=sinα

գ) 2sin(π/6+α)-cosα=2(sinπ/6cosα + cosπ/6 sinα)-cosα=2× cosα+√3sinα/2 -cosα=cosα+√3sinα-cosα=√3sinα

դ) √2 cos-2cos(π/4+α)=√2 cos-2(cosπ/4 cosα-sinπ/4 sinα)=√2cosα-(√2cosα-√2sinα)=√2cosα-√2cosα+√2sinα=√2sinα

Վարժ. 130

ա) √2 cos(3π/4 +α)+cosα / √2 cos(5π/4 -α)+sinα=√2(cos 3π/4 cosα-sin 3π/4 sinα)+cosα / √2(cos 5π/4 cosα+sin 5π/4 sinα)+sinα=-cosα-sinα+cosα/-cosα-sinα+sinα=-sinα/-cosα=tgα

բ) sin(2π/3 +α)+1/2 ×sinα / sin(7π/6 -α)+1/2 ×cosα= sin(2π/3 +α)+sinα/2 / sin(7π/6 -α)+cosα/2=√3 cosα / √3 sinα=cosα/sinα=ctgα

Վարժ. 131

ա) sin27°cos3°+cos27°sin3°=sin30°=1/2=0,5

բ) cos87°cos27°+sin87°sin27°=cos60°=1/2=0,5

Վարժ. 132

ա)(sin π/15 +cos π/10)² + (cos π/15 +sin π/10)²=3sinπ/15² + 2sinπ/15cos×π/10 + cosπ/10²+cosπ/15²+2cosπ/15×sinπ/10 + sin π/10²=2+( 1/2 -sinπ/30)+( 1/2 +sinπ/30)=2+ 1/2 -sinπ/30+1/2+sinπ/30=3

բ) (cos π/9 -cos 2π/9)² + (sin π/9 +sin 2π/9)²=1cos π/9² – 2cos π/9×cos 2π/9 + cos 2π/9² + sin π/9 + 2sin π/9×sin 2π/9 + sin 2π/9²=2-(cos π/9 + 1/2)+cos π/9 -1/2=2-cos π/9 – 1/2 + cos π/9 – 1/2=1

Առաջադրանք

Posted by jannanavoyan

a=22,5°

sina=sin45°/2=√1-cos45°/2=√1-√2/2/2=√2-√2/2/2=√2-√2/4=√2-√2/2

cosa=cos45°/2=√1+cos45°/2=√1+√2/2/2=√2+√2/2/2=√2+√2/4=√2+√2/2

tga=tg45/2=√1-cos45/1cos45=√1-√2/2/1+√2/2=√2-√2/2+√2/2=√2-√2/2+√2=√(2-√2)²/(2+√2)92-√2)=2-√2/√4-2=(2-√2*√2/√2*√2=2(√2-1)/2=√2-1

a=67.5

sin135/2=√-cos135/2=1-(-√2/2)/2=1√2/2/2=√2+√2/2=√2√/4=√2+2/2

cos135/2=√1+cos135/2=√1(-√2/2)/2=1-√2/2/2=√2-√2/2/2=2-√2/4=2-√2/2

Տնային աշխատանք

Posted by jannanavoyan

a=22,5° sina=sin45°/2=√1-cos45°/2=√1-√2/2/2=√2-√2/2/2=√2-√2/4=√2-√2/2 cosa=cos45°/2=√1+cos45°/2=√1+√2/2/2=√2+√2/2/2=√2+√2/4=√2+√2/2 tga=tg45/2=√1-cos45/1cos45=√1-√2/2/1+√2/2=√2-√2/2+√2/2=√2-√2/2+√2=√(2-√2)²/(2+√2)92-√2)=2-√2/√4-2=(2-√2*√2/√2*√2=2(√2-1)/2=√2-1 a=67.5 sin135/2=√-cos135/2=1-(-√2/2)/2=1√2/2/2=√2+√2/2=√2√/4=√2+2/2 cos135/2=√1+cos135/2=√1(-√2/2)/2=1-√2/2/2=√2-√2/2/2=2-√2/4=2-√2/2

Ֆունկցիաներ

Posted by jannanavoyan

Ֆունկցիան մաթեմատիկայում, երկու բազմությունների տարրերի միջև համապատասխանության կանոն է, ըստ որի առաջինի յուրաքանչյուր տարր համապատասխանում է երկրորդ բազմության մեկ և միայն մեկ տարրին։

Ֆունկցիայի մաթեմատիկական հասկացությունն արտահայտում է ինտուիտիվ գաղափար այն մասին, թե ինչպես է մի մեծությունն ամբողջությամբ որոշում մեկ այլ մեծության արժեքը։ Այսպիսով {\displaystyle x} $x$ փոփոխականի արժեքը եզակիորեն որոշում է {\displaystyle x^{2}} $x^{2}$ արտահայտության արժեքը, իսկ ամսվա արժեքը որոշում է դրան հաջորդող ամսվա արժեքը։ Ֆունկցիայի «կենցաղային» օրինակ է այն, որ յուրաքանչյուր մարդու կարելի է միանշանակ համապատասխանեցնել նրա կենսաբանական հորը։

Նմանապես, կանխորոշված ալգորիթմը, հաշվի առնելով մուտքային տվյալների արժեքը, որոշում է ելքային տվյալների արժեքը։

Հաճախ «ֆունկցիա» տերմինը հասկացվում է որպես թվային ֆունկցիա, այսինքն՝ ֆունկցիա, որը մի թվին համապատասխանեցնում է մյուսին։ Այս ֆունկցիաները հարմար է ներկայացնել գրաֆիկների տեսքով։

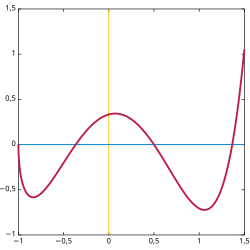
{\displaystyle {\begin{aligned}&\scriptstyle \\&\textstyle f(x)={\frac {(4x^{3}-6x^{2}+1){\sqrt {x+1}}}{3-x}}\end{aligned}}}

y=f(x),x∈X ֆունկցիայի գրաֆիկ անվանում են կոորդինատային հարթության այն (x;y) կետերի բազմությունը, որոնց համար y=f(x):

Օրինակ1. y=kx+b գծային ֆունկցիայի գրաֆիկն ուղիղ գիծ է: Ներքևում ցուցադրված է y=−1,5x−3 ֆունկցիայի գրաֆիկը:

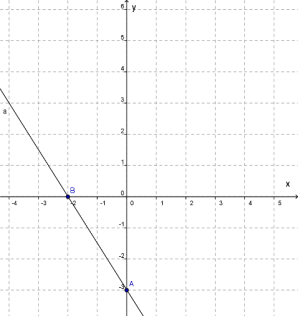
2. y=x² ֆունկցիայի գրաֆիկը կոչվում է պարաբոլ: Նրա տեսքը ցուցադրված է ներքևի նկարում:

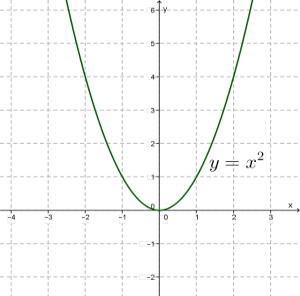
3. y=1/x ֆունկցիայի գրաֆիկը կոչվում է հիպերբոլ: Նրա տեսքը ցուցադրված է ներքևի նկարում:

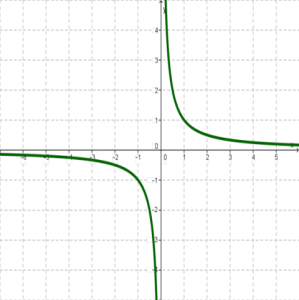
4. y=x−−√ ֆունկցիայի գրաֆիկն ունի հետևյալ տեսքը:

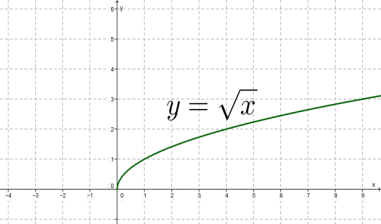
5. Հիշենք նաև y=|x| ֆունկցիայի գրաֆիկը:

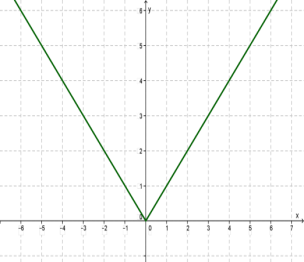
Հիշենք, որ ֆունկցիան ցանկացած արգումենտի համար պեքտ է ունենա միայն մեկ արժեք: Գրաֆիկի տերմիններով այս պահանջը նշանակում է, հետևյալը՝Կոորդինատային հարթության վրա գտնվող կորը հանդիսանում է որևէ ֆունկցիայի գրաֆիկ այն և միայն այն դեպքում, եթե օրդինատների առանցքին զուգահեռ ցանկացած ուղիղ կամ կորը չի հատում կամ հատում է միայն մեկ կետում:

Թվային ֆունկցիա

Ասում են, որ X թվային բազմությունում որոշված է f թվային ֆունկցիա, եթե այն (X) բազմության ամեն մի x թվի համապատասխանեցնում է y թիվ՝ y=f(x):

X բազմությունն անվանում են y = f(x) ֆունկցիայի որոշման տիրույթ:

f–ը բնութագրում է այն կանոնը, որով x փոփոխականի յուրաքանչյուր արժեքին (X) բազմությունից համապատասխանում է y փոփոխականի համապատասխան արժեքը:

x-ը անվանում են անկախ փոփոխական կամ արգումենտ, իսկ նրան համապատասխանող y թիվը՝ կախյալ փոփոխական կամ ֆունկցիայի արժեք x կետում:

f(x) ֆունկցիայի բոլոր արժեքների բազմությունն անվանում են y=f(x)

ֆունկցիայի արժեքների բազմություն:

fֆունկցիայի որոշման տիրույթն ընդունված է նշանակել D(f)-ով, իսկ արժեքների տիրույթը՝ E(f)-ով:

«Տրված է ֆունկցիա» ասելով հասկանում ենք, որ տրված է նրա D(f)

որոշման տիրույթը և նկարագրված է f կանոնը, որով որոշման տիրույթի ցանկացած x թվի համապատասխանության մեջ է դրվում y=f(x) թիվը:

Եթե ֆունկցիան տրված է բանաձևով և տրված չէ նրա որոշման տիրույթը, ապա ֆունկցիայի որոշման տիրույթը նրա թույլատրելի արժեքների բազմությունն է (ԹԱԲ):

f(x)=c, x∈X ֆունկցիան իր որոշման տիրույթի ցանկացած կետում ընդունում է միևնույն c արժեքը: Այսպիսի ֆունկցիան կոչվում է հաստատուն ֆունկցիա:

Մոնոտոն ֆունկցիաներ

y=f(x) ֆունկցիան կոչվում է աճող X⊂D(f) բազմության վրա, եթե ցանկացած x1 և x2 թվերի համար X բազմությունից, այնպիսին, որ x1<x2, կատարվում է f(x1)<f(x2) անհավասարությունը:

y=f(x) ֆունկցիան կոչվում է նվազողX⊂D(f) բազմության վրա, եթե ցանկացած x1 և x2 թվերի համար X բազմությունից, այնպիսին, որ x1<x2, կատարվում f(x1)>f(x2) անհավասարությունը:

Քանի որ ֆունկցիայի աճման և նվազման սահմանումների f(x1)<f(x2) և f(x1)>f(x2) անհավասարություններում բացառվում է հավասարության նշանը, ապա ֆունկցիաները նաև անվանում են խիստ աճող կամ խիստ նվազող: Եթե այդ անհավասարություններում թույլ տանք նաև հավասարության նշանը, ապա կգանք ֆունկցիայի աճման և նվազման ոչ խիստ սահմանումներին:

y=f(x) ֆունկցիան կոչվում է չնվազողբազմության վրա, եթե ցանկացած x1 և x2 թվերի համար X բազմությունից, այնպիսին, որ x1<x2, կատարվում է f(x1)≤f(x2) անհավասարությունը:

y=f(x) ֆունկցիան կոչվում է չաճող X⊂D(f) բազմության վրա, եթե ցանկացած x1 և x2 թվերի համար X բազմությունից, այնպիսին, որ x1<x2, կատարվում f(x1)≥f(x2) անհավասարությունը:

ա) f(x)={x2, եթե x≥00, եթե x<0 ֆունկցիան չնվազող է (−∞;+∞) բազմության վրա:

բ) f(x)={x2,եթե x<00, եթե x≥0 ֆունկցիան չաճող է (−∞;+∞) բազմության վրա:

Աճող, նվազող, չաճող, չնվազող ֆունկցիաները կոչվում են մոնոտոն (խիստ կամ ոչ խիստ) ֆունկցիաներ:

Քառակուսային ֆունկցիայի գրաֆիկը

y=ax2+bx+c, որտեղ a-ն, b-ն, c-ն իրական թվեր են և a≠0 կոչվում է քառակուսային ֆունկցիա:

Քառակուսային ֆունկցիայի գրաֆիկը պարաբոլ է:

Քառակուսային ֆունկցիայի D(f) որոշման տիրույթը բոլոր իրական թվերի բազմությունն է:

Քառակուսային ֆունկցիայի E(f) արժեքների բազմությունը կախված է պարաբոլի գագաթի y կոորդինատից և պարաբոլի ճյուղերի ուղղվածությունից:

a գործակիցը որոշում է պարաբոլի ճյուղերի ուղղվածությունը:

Եթե a>0, ապա ճյուղերը ուղղված են դեպի վերև:

Եթե a<0, ապա ճյուղերը ուղղված են դեպի ներքև: c գործակիցը ցույց է տալիս, թե որ կետում է պարաբոլը հատում Oy առանցքը:

Քառակուսային ֆունկցիայի գրաֆիկը կառուցելու համար պետք է՝

1) հաշվել պարաբոլի գագաթի կոորդինատները:

Աբսցիսը գտնում ենք x0=−b2a բանաձևով, իսկ y0 օրդինատը գտնում ենք՝ տեղադրելով x0 աբսցիսը ֆունկցիայի բանաձևի մեջ,

2) կոորդինատային հարթության վրա նշել գտնված գագաթը և տանել պարաբոլի համաչափության առանցքը,

3) որոշել պարաբոլի ճյուղերի ուղղվածությունը,

4) նշել պարաբոլի և Oy առանցքի հատման կետը,

5) ընտրելով x աբսցիսի անհրաժեշտ արժեքները, կազմել ֆունկցիայի արժեքների աղյուսակը: Լուծելով ax2+bx+c=0 քառակուսային հավասարումը, գտնում ենք պարաբոլի հատման կետերը Ox առանցքի հետ: Եթե D>0), ապա կա երկու հատման կետ:Եթե D<0, ապա պարաբոլը չի հատում Ox առանցքը:Եթե D=0, ապա պարաբոլի գագաթը գտնվում է Ox առանցքի վրա:

1. Կառուցենք y=x2−2x−1 ֆունկցիայի գրաֆիկը:

2. Կառուցենք y=−2×2+4x ֆունկցիայի գրաֆիկը:

Հաշվում ենք քառակուսային հավասարման արմատները՝ −2×2+4x=0x(−2x+4)=0x=0,−2x+4=0x=2×1=0x2=2 Գտնում ենք գագաթի կոորդինատները՝ x0=−42⋅(−2)=1y0=−2⋅12+4⋅1=2 Բավական է գտնել ֆունկցիայի արժեքը x=3 կետում՝ y=−2⋅(3)2+4⋅3=−18+12=−6 Համաչափ գտնում ենք, որ, եթե x=−1, ապա y=−6:

ՖՈՒՆԿՑԻԱ ՍԱՀՄԱՆԵԼՈՒ ԵՂԱՆԱԿՆԵՐ

Վերլուծական մեթոդ

Ֆունկցիան կարելի է սամանել՝ օգտագործելով վերլուծական արտահայտություն (օրինակ՝ բանաձև)։ Այս դեպքում այն նշվում է որպես համապատասխանություն հավասարության տեսքով։

Օրինակներ․

Ֆունկցիա, որը տրվում է մեկ բանաձևով․

{\displaystyle f(x)=x^{2}+a\sin(x)-{\frac {\pi }{\ln(x)}}\;\;(a\in \mathbb {R} );}

Անուղղակիորեն սահմանված ֆունկցիա․

{\displaystyle f(x)=y:x^{2}+y^{2}=R^{2}\;(R\in \mathbb {R} ,\;R\geqslant 0);}

Ոչ պաշտոնական սահմանում

$F$ ֆունկցիան, որը սահմանված է $X$ բազմության վրա $Y$ բազմության արժեքով, տրվում է «կանոնով», որ $X$ -ից յուրաքանչյուր x-ի տարրը համապատասխանում է $Y$ -ում գտնվող $f(x)$ տարրին և,ընդ որում, միայն մեկին։

Ընդունված նշաններ՝ $f:X\to Y$ , $X{\stackrel {f}{\longrightarrow }}Y$ , կրճատ գրում են $f\colon x\mapsto y$ կամ ուղղակի $y=f(x)$ .

$f:X\to Y$ գրաֆիկ անվանում են $\Gamma _{f}=\{\,(x,f(x))\in X\times Y\mid x\in X\,\}$ , որտեղ $X\times Y$ ուղիղ արտադրյալ։

Ընդհանուր առմամբ, ֆունկցիայի և դրա գրաֆիկի հասկացությունները համարժեք են, և քանի որ վերջինս մաթեմատիկորեն ավելի խիստ է սահմանված, ֆունկցիայի ֆորմալ (բազմությունների տեսության տեսանկյունից) սահմանումը նրա գրաֆիկն է։

$f:X\to Y$ ֆունկցիայի համար՝

$X$ բազմությունը կոչվում է առաջադրանքի բազմություն կամ ֆունկցիայի որոշման տիրույթ, որը նշվում է $D(f)$ կամ {\displaystyle \mathrm $\mathrm {dom} \,f$ -ով;
$Y$ բազմությունը կոչվում է ֆունկցիայի միջակայք, որը նշվում է $E(f)$ կամ $\mathrm {cod} \,f$ $\mathrm {ran} \,f$ )-ով;
$X$ բազմության յուրաքանչյուր $x$ տարր կոչվում է անկախ փոփոխական կամ ֆունկցիայի արգումենտ ;
$x$ կետին համապատասխանող $y=f(x)$ տարրը կոչվում է ֆունկցիայի մասնակի արժեք $x$ կետում։

Գրաֆիկական եղանակ

Ֆունկցիան կարող է սահմանվել նաև գրաֆիկի միջոցով։ Եթե $y=f(x_{1},x_{2},\ldots ,x_{n})\;$ — $n$ փոփոխականով իրական ֆունկցիա,ապա նրա գրաֆիկը կետերի բազմություն է $(n+1)$ -աչափ միջակայքում $\{(x_{1},x_{2},\ldots ,x_{n},f(x_{1},x_{2},\ldots ,x_{n})\}$ ։ Այս կետերի բազմությունը հաճախ հիպերմակերևույթ է։ Մասնավորապես, երբ $n=1$ ֆունկցիայի գրաֆիկը որոշ դեպքերում կարող է ներկայացվել երկչափ տարածության կորով։

Երեք կամ ավելի արգումենտներով ֆունկցիաների համար նման գրաֆիկական ներկայացումը կիրառելի չէ։ Այնուամենայնիվ, նույնիսկ նման ֆունկցիաները կարելի է ներկայացնել տեսողական կիսաերկրաչափական պատկերով (օրինակ, կետի չորրորդ կոորդինատների յուրաքանչյուր արժեքին տանք որոշակի գույն գրաֆիկի վրա, ինչպես դա տեղի է ունենում կոմպլեքս ֆունկցիաների գրաֆիկներում)։

$f(x)=x^{3}-3x$ գրաֆիկը

Արժեքների թվարկում

Վերջավոր բազմության վրա ֆունկցիան կարող է սահմանվել արժեքների աղյուսակով՝ ուղղակիորեն նշելով դրա արժեքները սահմանման տիրույթի յուրաքանչյուր տարրի համար։Այս մեթոդը օգտագործվում է, օրինակ, Բուլյան ֆունկցիաները սահմանելու համար։ Փաստորեն, այս մեթոդը նաև ֆունկցիայի գրաֆիկի սահմանումն է, եթե ֆունկցիայի գրաֆիկը $f\colon A\to B$ դիտարկենք որպես ձևի կարգավորված զույգերի բազմություն $(x,f(x))$ ։

ԸՆԴՀԱՆՈՒՐ ՀԱՏԿՈՒԹՅՈՒՆՆԵՐ

Բիեկցիա

Ֆունկցիան, որը միևնույն ժամանակ սուբեկտիվ և օբեկտիվ է, կոչվում է բիեկտիվ կամ փոխադարձ միանշանակ (կարճ՝ բիեկցիա)։

Հակադարձ ֆունկցիա

Եթե $f\colon X\to Y$ ֆունկցիան բիեկցիա է, ապա գոյություն ունի $f^{-1}\colon Y\to X$ , որի համար $x=f^{-1}(y)\;\Leftrightarrow y=f(x)$ ։

$f^{-1}$ ֆունկցիան այս դեպքում կոչվում է հակադարձ $f$ -ի նկատմամբ, բացի այդ, $f^{-1}$ նույնպես բիեկտիվ ֆունկցիա է։

Պարզաբանում

Քանի որ $f$ -ը ինեկցիա է, $f^{-1}$ ընդհանուր առմամբ ֆունկցիա է, $f$ սյուրեկցիայից իր հերթին հետևում է, որ $f^{-1}$ -ը տրված է $Y$ -ով։ $f^{-1}$ ֆունկցիան ինյեկտիվ է, քանի որ $f$ -ը ֆունկցիա է, և նրա սյուբեկտիվությունը հետևում է նրա սահմանումից։

Ընդհանուր առմամբ, արտապատկերումը, որն ունի հակադարձ, կոչվում է հակադարձ։ Հակադարձելիության հատկությունը միաժամանակ բավարարելն է երկու պայմանների․ $f^{-1}\circ f=\operatorname {id} _{X}$ և $f\circ f^{-1}=\operatorname {id} _{Y}$ ։

Ֆունկցիայի սահմանափակում և անընդհատություն

Դիցուք տրված է $f\colon X\to Y$ արտապատկերումը և $M\subsetneq X$ բազմությունը, որը $X$ բազմության խիստ ենթաբազմությունն է։

$g\colon M\to Y$ արտապատկերումը, որը $M$ -ի դեպքում ընդունում է նույն արժեքները, ինչ $f$ ֆունկցիան, կոչվում է $f$ ֆունկցիայի սահմանափակում $M$ բազմության վրա։

$f$ ֆունկցիայի սահմանափակումը $M$ բազմության վրա նշվում է հետևյալ կերպ․ $f{\big |}_{M}$ ։

Այս դեպքում սկզբնական $f$ ֆունկցիան, ընդհակառակը, կոչվում է $g$ ֆունկցիայի շարունակություն $X$ բազմություն վրա։

ՄՈՆՈՏՈՆՈՒԹՅՈՒՆ

Աճող և նվազող

Տրված է $f\colon M\subseteq \mathbb {R} \to \mathbb {R}$ ֆունկցիան, ապա

$f$ ֆունկցիան կոչվում է ոչ նվազող $M$ կետի նկատմամբ, եթե

y\Rightarrow f(x)\geq f(y),}”>

$f$ ֆունկցիան կոչվում է ոչ աճող $M$ կետի նկատմամբ, եթե

y\Rightarrow f(x)\leq f(y),}”>

$f$ ֆունկցիան կոչվում է աճող $M$ կետի նկատմամբ, եթե

y\Rightarrow f(x)>f(y),}”>

$f$ ֆունկցիան կոչվում է նվազող $M$ կետի նկատմամբ, եթե

Չաճող և չնվազող ֆունկցիաները կոչվում են (ոչ խիստ) միատոն, մինչդեռ աճող և նվազող ֆունկցիաները կոչվում են խիստ միատոն։ Կամայական ֆունկցիայի համար կարելի է գտնել մոնոտոնության միջակայքեր՝ որոշման տիրույթի ենթաբազմություններ, որոնց վրա ֆունկցիան այս կամ այն կերպ(խստությունը մեծ մասամբ ընտրվում է պայմանականորեն) մոնոտոն է։

Զույգություն

Ֆունկցիա $f\colon X\to \mathbb {R}$ կոչվում է կենտ, եթե տեղի ունի հետևյալ հավասարումը․

$f(-x)=-f(x),\quad \forall x\in X.$ Կենտ ֆունկցիայի գրաֆիկը համաչափ է սկզբնակետի նկատմամբ։

$f$ ֆունկցիան կոչվում է զույգ, եթե տեղի ունի հետևյալ հավասարումը․

$f(-x)=f(x),\quad \forall x\in X.$ Կենտ ֆունկցիայի գրաֆիկը համաչափ է օրդինատների առանցքի նկատմամբ։

Ֆունկցիայի էքստրեմումներ

Տրված է $f\colon X\to \mathbb {R}$ կետը և $x_{0}\in X$ , որը $f$ ֆունկցիայի համընդհանուր ներքին կետն է։

այդ դեպքում $x_{0}$ կետը կոչվում է մեծագույն արժեք, եթե գոյություն ունի $x_{0}$ կետի այնպիսի $M$ միջակայք, որտեղ՝ <img src=”https://wikimedia.org/api/rest_v1/media/math/render/svg/cd8b1c3894d3eabd301de35057d13414dcad7359″ alt=”{\displaystyle \forall x\in M,x\neq x_{0}\colon \quad f(x),
$x_{0}$ կետը կոչվում է փոքրագույն արժեք, եթե գոյություն ունի $x_{0}$ կետի այնպիսի $M$ միջակայք, որտեղ՝ f(x_{0})}”>։

Պարբերականություն

$f\colon M\to N$ ֆունկցիան կոչվում է պարբերական $T\not =0$ պարբերույթով, եթե ճիշտ է հետևյալ հավասարությունը․ $f(x+T)=f(x),\quad \forall x,x+T\in M$ .

Քանի որ $T$ պարբերույթով պարբերական ֆունկցիան պարբերական է նաև $nT\;(n\in \mathbb {N} )$ տիպի պարբերույթներով, ապա $T$ -ն ֆունկցիայի նվազագույն պարբերույթն է։

Եթե այդ հավասարությունը ճիշտ չէ ոչ մի $T\in M,\,T\not =0$ դեպքում, ապա $f$ ֆունկցիան կոչվում է ոչ պարբերական։

ՖՈՒՆԿՑԻԱՆ ԲԱԶՄՈՒԹՅՈՒՆՆԵՐԻ ՏԵՍՈՒԹՅԱՆ ՄԵՋ

Կախված նրանից, թե ինչպիսին է առաջադրման ոլորտի և նշանակումների տարածության բնույթը, տարբերակում են ոլորտների հետևյալ դեպքերը.

վերացական բազմություններ, որոնք առանց որևէ լրացուցիչ կառուցվածքի բազմություններն են,
բազմություններ, որենք օժտված է որոշակի կառուցվածքով։

1-ի դեպքում դիտարկվում են ընդհանուր ձևով արտապատկերումները և լուծվում են ամենատարածված հարցերը, օրինակ՝ բազմությունների համեմատումն ըստ հզորության․ եթե երկու բազմությունների միջև առկա է փոխմիարժեք արտապատկերում (բիեկցիա), ապա այդ բազմությունները կոչվում են էկվիվալենտ կամ համարժեք։ Սա թույլ է տալիս դասակարգել բազմությունները ըստ իրենց հզորության, և դրանցից ամենափոքրը, ըստ մեծացման, հետևյալն են.

վերջավոր բազմություններ, այստեղ բազմության հզորությունը համընկնում է տարրերի քանակի հետ,
հաշվելի բազմություններ, բնական թվերի բազմությանը համարժեք բազմություններ,
կոնտինուումի հզորության բազմություններ (օրինակ, թվային առանցքի հատվածը կամ թվային առանցքը)։

Այսպիսով, ստացվում են արտապատկերումների հետևյալ տեսակները՝ ըստ սահմանման տիրույթի հզորության.

վերջավոր ֆունկցիաներ՝ վերջավոր բազմությունների արտապատկերում,
հաջորդականություններ՝ հաշվելի բազմության արտապատկերում կամայական բազմության մեջ,
շարունակական ֆունկցիաներ՝ անհաշվելի բազմությունների արտապատկերումը վերջավոր , հաշվելի կամ անհաշվելի բազմությունների մեջ։

2-րդ դեպքում դիտարկման հիմնական առարկան բազմության մեջ տրված կառուցվածքն է (որտեղ բազմության տարրերն օժտված են որոշ լրացուցիչ հատկություններով, որոնք կապում են այդ տարրերը, օրինակ՝ խմբերում, օղակներում, վեկտորական տարածություններում) և այն, ինչ տեղի է ունենում այդ կառուցվածքի հետ արտապատկերման ժամանակ. եթե փոխմիարժեք արտապատկերման դեպքում պահպանվում են տվյալ կառուցվածքի հատկությունները, ապա ասում են, որ երկու կառուցվածքների միջև հաստատվում է իզոմորֆություն։ Այսպիսով, տարբեր բազմությունների մեջ տրված իզոմորֆ կառուցվածքները, ընդհանուր առմամբ, հնարավոր չէ տարբերվել, հետևաբար մաթեմատիկայում ընդունված է ասել, որ տվյալ կառուցվածքը դիտարկվում է «մինչև իզոմորֆիզմի ճշգրտությամբ»։

Գոյություն ունեն բազմաթիվ տարբեր կառուցվածքներ, որոնք կարելի է սահմանել բազմությունների մեջ։ Դրանց թվում են.

կարգի կառուցվածք – բազմության տարրերի մասնակի կամ գծային կարգը,
հանրահաշվական կառուցվածք – խմբոիդ, կիսախումբ, խումբ, օղակ, մարմին, ամբողջականության ոլորտ կամ դաշտ, որը սահմանված է բազմության տարրերի վրա,
մետրիկական տարածության կառուցվածք – բազմության տարրերի համար որոշվում է տարածության ֆունկցիան,
Էվկլիդեսյան տարածության կառուցվածք – բազմության տարրերի համար որոշվում է սկալյար արտադրյալը,
Տոպոլոգիական տարածության կառուցվածք – բազմության վրա տրվում է «բաց բազմությունների» ամբողջություն (որոնք չեն պարունակում իրենց սահմանը),
չափելի տարածության կառուցվածք – բազմության վրա տրվում է սկզբնական բազմության ենթաբազմությունների սիգմա հանրահաշիվը (օրինակ՝ տվյալ սիգմա հանրահաշիվը որպես ֆունկցիայի որոշման տիրույթ նշելով)։

Որոշակի հատկություն ունեցող ֆունկցիաներ կարող են չլինել այն բազմությունների վրա, որոնք չունեն համապատասխան կառուցվածք։ Օրինակ, այնպիսի հատկություն ձևակերպելու համար, ինչպիսին է բազմության վրա սահմանված անընդհատ ֆունկցիան, այդ բազմության վրա անհրաժեշտ է սահմանել տոպոլոգիական կառուցվածք։

Ընդհանրացում

Մասամբ սահմանված ֆունկցիաներ

$X$ բազմությունից $Y$ բազմության վրա $f$ մասամբ սահմանված ֆունկցիա է կոչվում $f\colon X'\to Y$ ֆունկցիան $X'={\rm {Dom}}f\subsetneq X$ որոշման տիրույթով։

Որոշ հեղինակներ ֆունկցիա ասելով կարող են նկատի ունենալ միայն դրա սահմանափակումը, այնպես որ «սահմանափակ» որոշման տիրույթում ֆունկցիան ամբողջությամբ սահմանված է։ Սա ունի իր առավելությունները, օրինակ՝ հնարավոր է $f\colon \mathbb {R} \to \mathbb {R}$ գրառումը, որտեղ $f(x)=1/x$ , այդ դեպքում նկատի է առնվում՝ $\mathop {\rm {Dom}} f=\mathbb {R} \backslash \{0\}$ ։

Բազմարժեք ֆունկցիաներ

Արգումենտի տրված արժեքին պետք է համապատասխանի ֆունկցիայի միայն մեկ արժեք, որը կապված է բուն ֆունկցիայի սահմանման հետ։ Բայց, չնայած դրան, հաճախ հնարավոր է հանդիպել այսպես կոչված բազմարժեք ֆունկցիաների։ Իրականում սա միայն այնպիսի ֆունկցիայի հարմար նշանակման ձև է, որի արժեքների տիրույթը ինքնին բազմությունների ընտանիք է։

Դիցուք $f\colon X\to \mathbb {B}$ , որտեղ $Y$ բազմության ենթաբազմությունների ընտանիքն է։ Այդ դեպքում $f(x)$ բազմություն է ցանկացած $x\in X$ դեպքում։

Ֆունկցիան միարժեք է, եթե արգումենտի յուրաքանչյուր արժեքի համապատասղանում է ֆունկցիայի մեկ արժեք։ Ֆունկցիան բազմարժեք է, եթե արգումնենտի գոնե մեկ արժեքի համապատասխանում են ֆունկցիայի երկու կամ ավելի արժեքներ։

Շիրակացին մեր տներում

Posted by jannanavoyan

ՇՓաստեր իրակացու մասին

▪︎Անանիա Շիրակացու պատվին մետաղադրամ

▪︎Զբաղվել է փիլիսոփայությամբ, աստղագիտությամբ, աշխարհագրությամբ, մաթեմատիկայով, տոմարագիտությամբ, ալքիմիկոսությամբ։

▪︎Շիրակացին բացատրում էր տարվա եղանակների, գիշերվա ու ցերեկվա առաջացումը։

▪︎Նա տվել է Հայաստանի միջին լայնության համար ստվերաչափ կազմելու կանոնը։

Խնդիրներ

▪︎Իմ մերձավոր մարդկանցից մեկը Մեկնելով Բահլ՝ շահաբեր գնով մարգարիտ ձեռք բերեց։ Տուն վերադառնալիս, հասնելով Գանձակ, նա իր գնած մարգարիտի կեսը վաճառեց հատը 50 դրամով։ Գալով Նախիջևան՝ վաճառեց նրա քառորդ մասը, հատը 70 դրամով, ապա հասնելով Դվին՝ վաճառեց նաև այդ մարգարիտի 1/12 մասը՝ հատը 50 դրամով։ Երբ նա եկավ մեզ մոտ՝ Շիրակ, նրա մոտ մնացել էր ընդամենը 24 հատ մարգարիտ։ Արդ, այդ մնացածով իմացի՛ր, թե ընդամենը քանի մարգարիտ էր գնել նա և քանի՞ դրամ էր ստացել վաճառած մարգարիտներից։

լուծում
1/2+1/4+1/12=10/12
12/12-10/12=2/12
12/12:2/12=6
24×6=144
144:2=72
72×50=3600
144:4=36
36×70=2520
144:12=12
12×50=600
600+2520+3600=6720
Պատ՝․144 մարգարիտ, 6720 դրամ։

▪︎Ես իմ ուսուցչից լսեցի, թե գողերը, մտնելով Մարկիանոսի գանձարանը, գանձի կեսը և 1/4-ը գողացան։ Գանձապահները ներս մտնելով՝ գտան 421 կենդինար( 1 կենդինարը հավասար է 7200 դահեկանի) և 3600 դահեկան։ Արդ իմացի՛ր, թե ամբողջ գանձը որքա՞ն էր։

լուծում

1/2+1/4=3/4
4/4:1/4=4
421×7200=3031200
3031200+3600=3034800
3034800×4=12139200
12139200:7200=1686

Ֆլեշմոբ

Posted by jannanavoyan

2-րդ մակարդակ

Անուն Ժաննա

Ազգանուն Նավոյան

Դասարան 1-3 կուրս

Դպրոց քոլեջ

1. Գտի՛ր օրինաչափությունը և լրացրո՛ւ դատարկ վանդակը:

Подпись отсутствует
2. Երկնիշ թվի թվանշանների արտադրյալը 21 է: Որքա՞ն է այդ թվի թվանշանների գումարը:

21= 3 * 7 3 + 7 = 10

3. Երեք հաջորդական զույգ թվերի գումարը 336 է։ Գտի՛ր այդ թվերից ամենամեծը։

110 + 112 + 114 = 336 Պատ․՝114։

4. Մարիամն ամեն օր գրում է այդ օրվա ամսաթիվն ու ամիսը, այնուհետև հաշվում է թվանշանների գումարը: Օրինակ՝ մարտի 26-ը գրում է այսպես՝ 26.03, գումարը կլինի՝ 2+6+0+3=11: Մարիամի ստացած ամենամեծ գումարը ո՞րը կլինի։

20․09 2 +9+ 0 +9= 20

5. Ճագարն ուներ 20 գազար: Ամեն օր նա ուտում էր երկու գազար: Շաբաթվա ո՞ր օրն էր նա սկսել ուտել իր գազարները, եթե 11-րդ գազարը կերել էր երեքշաբթի օրը։

Հինգշաբթի

6. Փուչիկները վաճառվում են տարբեր փաթեթներով, որոնցից յուրաքանչյուրը պարունակում է՝ 5, 10 կամ 25 հատ փուչիկ: Ամենաքիչը քանի՞ փաթեթ պետք է գնի Մարինեն, եթե նա ուզում է գնել ճիշտ 70 փուչիկ:

25 +25 +10 +10 =70 1պ․+ 1պ․ +1պ․+ 1պ․ =4

7. Առաջին կանգառում ավտոբուսից իջան 3 ուղևոր, երկրորդ կանգառում բարձրացան 6 ուղևոր, երրորդ կանգառում իջան 4 ուղևոր և բարձրացան 3 ուղևոր։ Արդյունքում ավտոբուսում մնացին 15 ուղևոր։ Սկզբում ավտոբուսում քանի՞ ուղևոր կար։

-3+6-4+3=2 15-2=13

8. Երկու դարբին միասին աշխատելով՝ որոշակի աշխատանք կարող են կատարել 8 օրում։ Երկրորդ դարբինը միայնակ քանի՞ օրում կարող է կատարել այդ աշխատանքը, եթե առաջին դարբինը այն կատարում է 12 օրում։

Մոնիկան ունի տարբեր գույնի երեք արկղ՝ սպիտակ, կարմիր և կանաչ: Դրանցից մեկում տանձ է, մյուսում՝ խնձոր, մեկն էլ դատարկ է: Ո՞ր գույնի արկղում է տանձը, եթե հայտնի է, որ այն կա՛մ սպիտակ, կա՛մ կարմիր արկղում է, իսկ խնձորը` ո՛չ սպիտակ, ո՛չ էլ կանաչ արկղում։

Կարմիր

10. Դասարանի բոլոր 30 սովորողները ցանկություն հայտնեցին մասնակցելու ֆուտբոլի կամ բասկետբոլի մրցումներին: Նրանցից 15-ը ցանկություն հայտնեց մասնակցելու ֆուտբոլի մրցումներին, իսկ 20-ը` բասկետբոլի: Քանի՞ սովորող մասնակցեց և՛ ֆուտբոլի, և՛ բասկետբոլի մրցումներին:

Պատ․՝ 10։

Մաթեմատիկայի նոյեմբերյան ֆլեշմոբ, 3-րդ մակարդակ

Posted by jannanavoyan

Անուն* Ժաննա

Ազգանուն * Նավոյան

Դասարան* 1֊3 կուրս

Դպրոց * քոլեջ

Երկու թվերի ամենամեծ ընդհանուր

բաժանարարը հավասար է 18-ի: Կարող

է այդ թվերի ամենափոքր ընդհանուր

բազմապատիկը հավասար լինի 240-ի:

Ոչ չի կարող։

Սեղանին դրված են

մետաղադրամների 6 խումբ, ընդ որում առաջին խմբում կա 1 մետաղադրամ, երկրորդում՝ 2, երրորդում՝ 3, չորրորդում 4. հինգերորդում՝ 5, իսկ վեցերորդում` 6 մետաղադրամ: Թույլատրվում է յուրաքանչյուր քայլում խմբերից որևէ երկուսում ավելացնել մեկական մետաղադրամ։ Հնարավոր է, որ ինչ-որ քայլից հետո բոլոր խմբերում լինեն հավասար քանակությամբ մետաղադրամներ։

Ոչ, հնարավոր չէ:

20սմ կողով խորանարդը ներկելու համար պահանջվեց 20 գրամ ներկ: Քանի գրամ ներկ է անհրաժեշտ 40սմ

կողով խորանարդը ներկելու համար։

40գրամ

Արամն ու Բաբկենը միասին

հավաքեցին 3 անգամ ավելի շատ սունկ,

քանԳեղամը, Բաբկենն ու Գեղամը միասին 4 անգամ ավելի շատ, քան` Արամը: Բաբկենն ավելի շատ սունկ հավաքեց, թե՞ Արամն ու Գեղամը միասին:

Բաբկենը:

Վարդանը գումարեց ամսվա բոլոր

հինգշաբթի օրերի ամսաթվերը և ստացավ 855 Ի՞նչ թիվ կստանար Վարդանը, եթե գումարեր այդ ամսվա բոլոր ուրբաթ օրերի ամսաթվերը։

Լուծում

25+18+11+4= 58

Պատ.՝58

ձ. Ինչ–որ բնական թիվ 21-ի բաժանելիս քանորդում և մնացորդում ստացվում են հավասար թվեր: Այդ նույն թիվը 33-ի բաժանելիս քանորդում և մնացորդում նույնպես ստացվում են հավասար թվեր։ Գտիր այդ թիվը:

Мой ответ

Ամանում դրված է տանձ և խնձոր: Երբ երեխաները կերան խնձորի 1/3 մասը,

ամանում մնաց ամբողջ մրգի 3/4 մասը։

Սկզբում ամանում եղած մրգերից որն էր

շատ և քանի անգամ:

Տանձը 2անգ ավելի շատ է քան խնձորը:

Հարթության վրա տրված են նույն

շառավղով երեք շրջանագծեր: Գտի՛ր AK

+KC+KE աղեղների աստիճանային

չափերի գումարը:

Мой ответ

Արամը ոտքով տնից գնում է դպրոց։ Տնից դուրս գալուց 7 րոպե հետո նրան մնում է անցնելու ևս 640մ, իսկ 11 րոպե հետո՝ ևս 32–մ: Որքա՞ն է տնից դպրոց

եղած հեռավորությունը (ամբողջ

Ճանապարհին արագությունը

հաստատուն է մնացել):

Լուծում

7p-640d 4p – 3200

11n 320d 1n-80 d 5600+640d=12000

Պատ.` 1200մ

ABCD քառակուսու կողմը 10 է: BC

կողմի վրա վերցված է M կետն այնպես, որ BM:MC=4:6, իսկ CD կողմի վրա վերցված է N կետն այնպես, որ CN:ND=8:2: Գտիր AMN եռանկյան

մակերեսը:

Մխիթար Սեբաստացի կրթահամալիր 3-2 կուրս

Նավոյան Ժաննա

Մաթեմատիկա

Տնային աշխատանք

Տնային աշխատանք

Կրկնակի անկյան սինուսն ու կոնսինուսն, տանգեսն ու կոտանգես

Տնային աշխատանք

Առաջադրանք

Տնային աշխատանք

Ֆունկցիաներ

Շիրակացին մեր տներում

Ֆլեշմոբ

Մաթեմատիկայի նոյեմբերյան ֆլեշմոբ, 3-րդ մակարդակ